地学自主ゼミ：3.遠心力のはなし

地学自主ゼミ（2003年度版）

　ここでちょっと寄り道をして、遠心力のはなしをします。地球上のいろいろな現象を説明するのに遠心力について知っていると便利である。

　まず、角速度について。　・・・1秒間にどれだけの角度回ったかをあらわす。
　例えば、ある物体が T 秒間かかって円を一周（＝ 2π rad）したら、角速度ωは、

　これが地球だったら一周するのに一日かかるから、

である。

　角速度ωで、半径 r の円軌道を描いているときは、各瞬間に物体の運動方向は、その点における円周の接線方向で、その速度は次のようになる。

　　←　円周が 2πr で、これを T 秒で進むから。

　さて、ある時刻 t における物体の位置を P とすると、

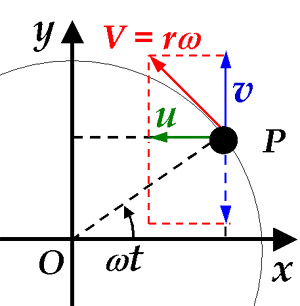
図で、動径 OP のなす角を ωt として、　　←　速さ（角速度）× 時間＝距離
速度 V の x 成分と y 成分はそれぞれ、

x 成分　：　

y 成分　：　

で、それぞれの方向の加速度は、上式を時間で微分すれば求まる。

x 成分　：　

y 成分　：　

　これらの合ベクトルを求めると、次のようになる。

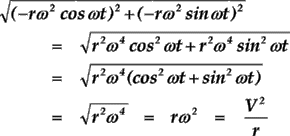
　これが、円運動の加速度で、ベクトル的に円の中心に向かう事がわかる（ x・y 成分が負で、その合ベクトルだから）。

　これを踏まえて、地球上のある地点に存在する物体にかかる遠心力について考えると、この地点は地球の自転軸を中心に円運動していることになり、その地点の緯度をφ°、地球の半径を R とすれば、回転の半径は R cosφ° である。物体の質量を m とすれば、この物体の運動方程式は、

となって、地球上での遠心力が求められた。

■　宿題　■

- 問 -: 　地球を半径 6400km の球とする。自転周期を 24 時間、極における重力加速度の大きさを 10ms^-2 とすると、地球の赤道上の重力加速度の大きさは、極におけるそれよりも何 % 小さいか。